Jacques van Helden
2019-01-16
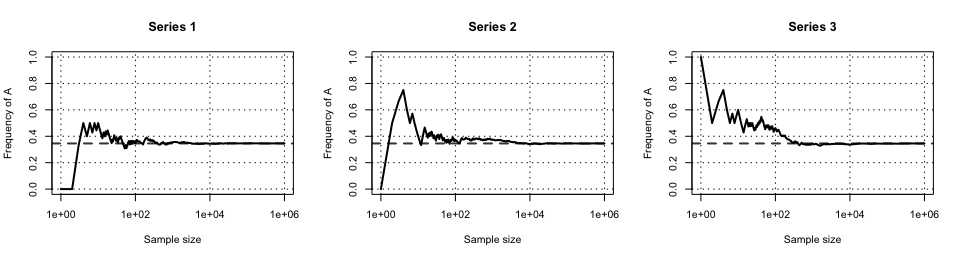
Lors d’une expérience aléatoire, la probabilité d’un événement \(A\) est la limite de sa fréqunce de réalisation quand le nombre d’essais tend vers l’infini.
\[\operatorname{P}(A) = \lim_{n \to \infty}\frac{n_{A}}{n}\]
Fréquences de A lors du tirage (avec remise) de positions aléatoires dans le génome de Mycoplasma genitalium.
Supposons qu’on tire des éléments dans un ensemble fini, en considérant certains tirages comme des succès (\(A\)). Dans cette situation, la probabilté est définie comme le rapport entre le nombre de tirages pouvant être considérés comme des succès (\(n_A\)) et le nombre total de tirages possibles (\(n\)).
\[\operatorname{P}(A) = \frac{n_A}{n}\]
Exemple: sélection aléatoire de 4 cartes dans un jeu de 52 cartes. Quelle est la probabilité d’avoir un carré (4 cartes identiques) ?
Le jeu de carte comporte 13 valeurs (As, 2, 3, …, Dame, Roi), il y a donc 13 possibilités d’obtenir un carré: \(n_A = 13\).
Le nombre total de tirages de 4 cartes parmi 52 est fourni par le coefficient binomial: \[n = \binom{52}{4} = 270725\]
\[\operatorname{P}(A) = \frac{n_A}{n} = \frac{13}{\binom{52}{4}} = \frac{13}{270725} = 4.8\times 10^{-5}\]
On désigne des événements de mutuellement exclusifs quand la réalisation de l’un rend impossible la réalisation des autres. Leur probabilité jointe (\(A_1\) et \(A_2\)) est donc nulle.
\[A_1,A_2 \text{mutuellement exclusifs} \iff \operatorname{P}(A_1 \land A_2) = 0\]
Le symbole \(\land\) correspond au et logique.
Si deux événements \(A_1\) et \(A_2\) sont mutuellement exclusifs, la probabilité de réalisation de l’un ou de l’autre est la somme de leurs probabilités.
\[\operatorname{P}(A_1 \land A_2) = 0 \iff \operatorname{P}(A_1 \lor A_2) = \operatorname{P}(A_1) + \operatorname{P}(A_2)\]
Un ensemble d’événements \({A_1, A_2, \ldots, A_m}\) sont dit complémentaires s’ils sont mutuellement exclusifs et exhaustifs (il n’existe pas d’événement possible en dehors de l’ensemble).
La probabilité de l’union d’événements complémentaires vaut 1.
\[A_1, A_2, \ldots A_m \text{complementary} \Rightarrow \operatorname{P}(A_1 \lor A_2 \lor \ldots \lor A_m) = \operatorname{P}(A_1) + \operatorname{P}(A_1) + \ldots + \operatorname{P}(A_m) = 1\]
Deux événements sont stochastiquement indépendants si la réalisation de l’un n’affecte pas la probabilité de réalisation de l’autre.
La probabilité jointe d’une série d’événements indépendants est le produit de leurs probabilités.
\[\begin{aligned} A_1, A_2, \ldots A_m \text{ independent } \nonumber\\ \Rightarrow \operatorname{P}(A_1 \land A_2 \land \ldots \land A_m) = \operatorname{P}(A_1) \operatorname{P}(A_2) \ldots \operatorname{P}(A_m) \end{aligned}\]
\[\operatorname{P}(A \lor B) = \operatorname{P}(A) + \operatorname{P}(B) - \operatorname{P}(A \land B)\]
Un essai de Bernoulli est une expérience aléatoire qui peut résulter en deux événements possibles, dénommés succès et échec, chacun étant associé à une probabilité.
Un schéma de Bernoulli est une série d’essais qui satisfont les conditions suivantes:
Indépendance: le résultat d’un essai n’affecte pas les probabilités de succès de l’essai suivant.
La probabilité de succès est identique pour chacun des essais.
On peut généraliser la définition précédente en considérant une série d’essais pouvant résulter en un nombre finis de résultats possibles, associés chacun à une probabilité. Si les essais successifs sont indépendants et les probabilités des événements constantes au fil des essais, on parle de schéma de Bernoulli généralisé.
Exemple: modèle de probabilité des nuclétides dans le génome de la levure, basé sur les fréquences nucléotidiques.
| Résidu | Occurrences génomiques | Fréquence génomique |
|---|---|---|
| A | 3766191 | 0.3098064564636 |
| C | 2320522 | 0.1908858838986 |
| G | 2316991 | 0.1905954242278 |
| T | 3752889 | 0.3087122354100 |
Dans le cadre d’un tirage aléatoire, on va considèrer que chaque résidu a une probabilité particulière:
\(\operatorname{P}(A) = 0.31\), \(\operatorname{P}(C) = 0.19\), \(\operatorname{P}(G) = 0.19\), \(\operatorname{P}(T) = 0.31\).
Le schéma de Bernoulli présente un intérêt évident: sa facilité d’utilisation. Cependant il n’est pas très approprié pour modéliser les successions de résidus dans les séquences macromoléculaires, pour plusieurs raisons.
Les modèles de Markov permettent une modélisation plus fine des séquences biologiques, en exprimant la dépendance entre résidus voisins.