Sampling and estimation
Probabilités et statistique pour la biologie (STAT1)
Jacques van Helden
2019-10-04
Contenu
Dans ce cours, nous aborderons un problème fondamental en statistique: comment estimer les paramètres d’une population à partir d’un échantillon ?
Mots-clés:
- population, échantillon,
- estimateurs de la tendance centrale (moyenne, médiane, mode)
- estimateurs de dispersion (variance, écart-type, espace inter-quartile)
- échantillonnage de la moyenne (erreur standard)
- intervalle de confiance autour de la moyenne
- distributions: normale, Student
- théorème central limite
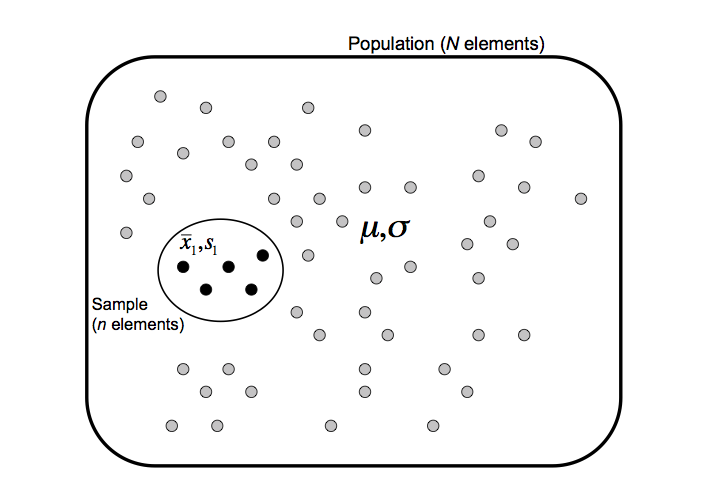
Population et échantillon
On s’intéresse à des propriétés mesurables d’une population (finie ou infinie) qu’il est impossible de couvrir de façon exhaustive (coût, temps, mesures destructives). On prélève un échantillon, sur lequel on peut mesurer des paramètres (moyenne, écart-type).
On estime les paramètres de la population (\(\mu\), \(\sigma\)) à partir des paramètres d’échantillon (\(\bar{x}\), \(s\)).
Population et échantillon
- \(N\), \(\mu\), \(\sigma\): paramètres de population (nombre d’individus, moyenne, écart-type).
- \(n\), \(\bar{x}\), \(s\): paramètres d’échantillon (nombre d’individus, moyenne, écart-type).
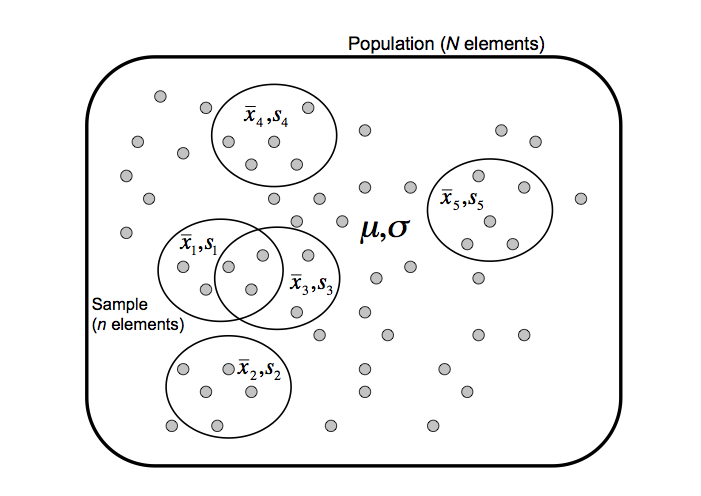
Population et échantillons
Problème général de l’estimation: si l’on avait choisi un autre échantillon, on disposerait de paramètres différents. Dès lors, comment évaluer la fiabilité de nos estimateurs ?
Paramètres classiques
Moyenne: paramètre de tendance centrale
\[\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i\]
Variance: : paramètre de dispersion
\[s^2 = \frac{1}{n}\sum_{i=1}^n (x_i -x)^2\]
Ecart-type: : paramètre de dispersion (plus pratique que la variance, car mêmes unités que les observations, et que la moyenne).
\[s = \sqrt{\frac{1}{n}\sum_{i=1}^n (x_i -x)^2}\]
Paramètres robustes
Les paramètres classiques (moyenne, variance) sont sensibles à la présence de valeurs aberrantes (“outliers” en anglais). En particulier, la variance est très affectée par la présence de quelques valeurs aberrantes, car ces valeurs sont prises au carré.
Alternative: se baser sur les quartiles.
\(\tilde{x}\): la médiane est la plus petite valeur supérieure ou égale à la moitié des valeurs observées. La médiane est un paramètre robuste de tendance centrale.
\(Q_1\): le premier quartile, la valeur supérieure ou égale à \(25\%\) des valeurs observées.
\(Q_3\): le troisième quartile, la valeur supérieure ou égale à \(75\%\) des valeurs observées.
\(\text{IQR} = Q_3 - Q_1\): l’écart inter-quartile (inter-quartile range): est un estimateur robuste de la dispersion.
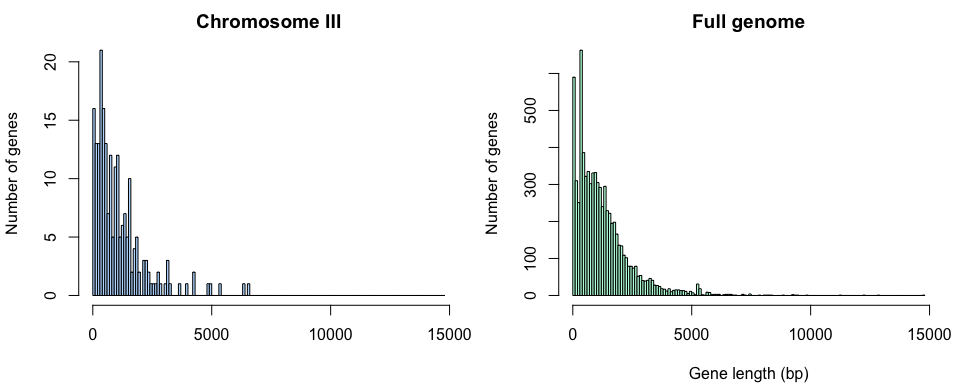
Exemple historique: génome de la levure
- 1992: publication du premier chromosome eucaryote complet, le 3ème chromosome de la levure.
- 1996: publication du génome complet.
Sur base des gènes dU 3ème chromosome (échantillon) on peut estimer la taille moyenne d’un gène de levure.
Questions:
La moyenne d’échantillon (chromosome III) permettait-elle de prédire la moyenne de la population (génome complet) ?
Cet échantillon peut-il être qualifié de “simple et indépendant” ?
Distribution des tailles de gènes
Exemples actuels
Dans chaque cas, définissez la ou les populations, et posez-vous les questions concernant la validité de l’échantillonnage (simple, indépendant, représentatif, …).
Profils transcriptomiques de patients: 40 cas de leucémie myéloide aigue (AML) et 40 cas de leucémie lymphoblasique eaigue (ALL).
Etude d’association à échelle génomique: SNPs de 2000 cas (diabète de type 2) et 3000 contrôles (pas de diabète.
Paramètres de population
Par convention, nous utiliserons les symboles suivants pour les paramètres calculés sur la population entière.
- \(X\): variable aléatoire représentant toutes les valeurs possibles d’une observation (par exemple l’ensemble des nombres réels, ou naturels).
- \(x_i\): valeur particulière de cette variable pour le \(i^{ème}\) individu d’une population.
| Taille (nombre d’individus) |
\(N\) |
| Moyenne |
\(\mu = \frac{1}{N}\sum_{i=1}^{N} x_i\) |
| Variance |
\(\sigma^2 = \frac{1}{N}\sum_{i=1}^{N} (x_i - \mu)^2\) |
| Ecart-type |
\(\sigma = \sqrt{\sigma^2}\) |
Paramètres d’échantillons
Par convention, nous utiliserons les symboles suivants pour les paramètres calculés sur un échantillon.
| Effectif (nombre d’individus) |
\(n\) |
| Observations |
\(x = \{x_1, x_2, \cdots, x\_n \}\) |
| Moyenne |
\(\bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_i\) |
| Variance |
\(s^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})^2\) |
| Ecart-type |
\(s = \sqrt{s^2}\) |
La barre au-dessus d’un symbole de variable dénote la moyenne.
Jeux de données simulés
Avant d’analyser les données réelles, jouons avec des jeux de données générés selon un modèle probabilise donné. Nous conrôlons ainsi tous les paramètres, et pouvons évaluer la fiabilité des estimateurs.
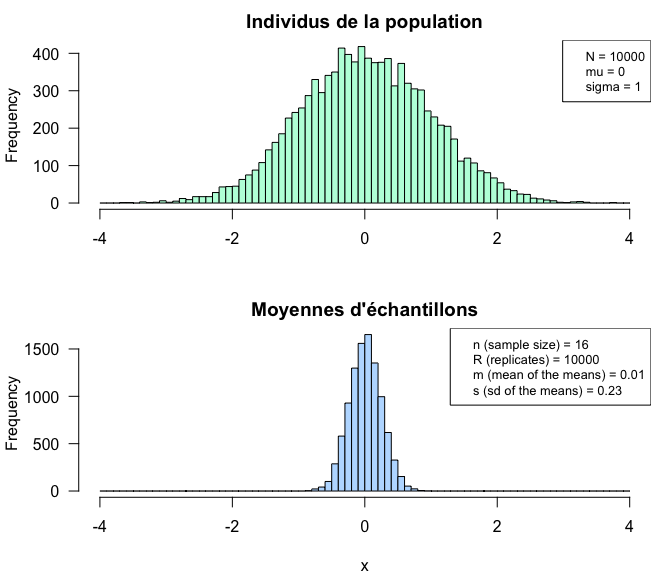
Moyennes d’échantillons
On prélève un échantillon d’effectif \(n=16\) (nombre d’éléments) dans une population de taille \(N=10^{4}\).
La population suit une distribution gaussienne de moyenne \(\mu=0.0117522\) et d’écart-type \(\sigma=0.9884815\).
Répétons l’échantillonnage un grand nombre de fois (\(R = 10^{4}\)). Pour chaque échantillon, calculons la moyenne, et étudions la distribution de ces moyennes.
Distribution d’échantillonnage de la moyenne
Espérance de la moyenne d’échantillon
Non biaisée: l’espérance de la moyenne d’échantillon est égale à la moyenne d’échantillon: si on prélèvait un nombre infini d’échantillons et qu’on calculait leurs moyennes (\(\bar{X}\)), la moyenne de ces moyennes de la population (\(\mu\)).
\(<\bar{X}> = \mu\)
Variance de la moyenne d’échantillon
Dispersion: la variance de la moyenne d’échantillon diminue avec l’effectif.
\(\sigma^2_{\bar{X}} = \frac{\sigma^2}{n}\)
\(\sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}}\)
Convergence
Quand la taille de l’échantillon augmente, la moyenne d’échantillon (\(\bar{X}\)) converge vers la moyenne de la population (\(\mu\)).
Cette convergence est d’autant plus rapide que l’effectif (\(n\)) est grand.
L’imprécision (qu’on peut mesurer par l’écart-type) diminue avec la racine carrée de l’effectif.
En pratique, ceci signifie que si l’on veut doubler la précision d’une estimation de moyenne, il faut quadrupler la taille d’échantillon !
Estimateurs robustes versus convergence
Note: la moyenne d’échantillon (\(\bar{x}\)) converge plus rapidement que la médiane (\(\tilde{x}\)) vers la moyenne de population (\(\mu\)). De même, l’écart-type converge plus rapidement que l’espace interquartile.
Si l’on veut utiliser des paramètres robustes aux valeurs aberrantes (\(\tilde{x}\), \(\text{IQR}\)), il faut donc s’assurer qu’on dspose d’un échantillon d’effectif (\(n\)) suffisant.
Distribution normale
Egalement appelée distribution gaussienne.
Densité de probabilité:
\[f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}(\frac{x - \mu}{\sigma})^2}\]
** Distribution normale standard**
La distribution normale standard \(\mathcal{N}(1,0)\) est une normale de moyenne \(\mu=0\) et d’écart-type \(\sigma=1\).
Standardisation
Théorème central limite
La somme de variables aléatoires indépendantes et identiquement distribuées tend vers une distribution gaussienne.
Démo au cours
Variance d’échantillon
Variance d’échantillon.
\[s^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})^2\] La variance d’échantillon constitue-t-elle un bon estimateur de la variance de la population ? Non. Pourquoi ?
Biais de la variance d’échantillon
L’espérance de la variance d’échantillon diffère de la variance de la population.
\[<s^2> = \sigma^2 \cdot \frac{n-1}{n} < \sigma^2\]
\(s\) est un estimateur biaisé de \(\sigma\):
Estimation non-biaisée de la variance
Pour estimer la variance de la population, on effectue une correction du biais mentionné.
\[\hat{\sigma^2} = \frac{n}{n-1} s^2 = \frac{1}{n-1}\sum_{i=1}^{n} (x_i - \bar{x})^2\]
Intervalle de confiance autour de la moyenne
On dispose d’une moyenne d’échantillon \(\bar{x}\).
On ignore la moyenne de population \(\mu\), mais on saite que la distribution de moyennes d’échantillon prélevés dans cette population suit une certaine distribution.
Sur cette base, on peut calculer un intervalle de confiance, qui est limité par les valeurs au-delà desquelles, si \(\mu\) s’y trouvait, la probabilité d’obtenir la moyenne observée serait inférieure à une probabilité \(\alpha\) donnée (exemple: \(\alpha = 0.05\)).
Niveau de confiance: \(1 - \alpha\) (exemple: \(1-\alpha= 0.95\)).
Distribution de Student
Démo: forme de la distribution de Student en fonction de \(\nu\).