Approvoiser la P-valeur – Corrections pour les tests multiples
Probabilités et statistique pour la biologie (STAT1)
Jacques van Helden
2018-11-23
What is a P value?
There are hundreds of published articles arguing about the correct use, misinterpretation and misuse of the P value.
In 2016, the American Statistical Association published an article to address the question of good use and misuse of thresholds on the P value.
“Informally, a p-value is the probability under a specified statistical model that a statistical summary of the data (e.g., the sample mean difference between two compared groups) would be equal to or more extreme than its observed value.”
Source: The ASA’s Statement on p-Values: Context, Process, and Purpose (2016)
“De manière informelle, la probabilité critique (”P valeur“) est la probabilité, étant donné un modèle statistique, qu’une statistique qui décrit les données (par exemple la différence de moyenne entre deux groupes comparés) soit égale ou plus extrême que la valeur observée.”"
What is the right threshold on P value?
- Q: Why do so many colleges and grad schools teach \(p = 0.05\)?
- A: Because that’s still what the scientific community and journal editors use.
- Q: Why do so many people still use \(p = 0.05\)?
- A: Because that’s what they were taught in college or grad school
Source: The ASA’s Statement on p-Values: Context, Process, and Purpose (2016)
Problème: occurrences de k-mères
We counted the occurrences of all octanucleotides (\(k = 8\)) in a sequence of \(L = 100,000\) base pairs (single strand counts). The sequence contains \(x = 6\) occurrences of GATTACCA.
Assuming equiprobable and independent nucleotides, is this k-mer over-represented in the sequence?
Modelling the problem
Prior probability of the k-mer: \(p = 0.25^8 = 0.0000153\)
Number of possible positions: \(N <- L - k + 1 = 100,000- 8+ 1 = 99,993\)
Expected occurrences : \(<X> = N \cdot p = 99,993 \cdot 0.0000153= 1.53\)
Over-representation
We observe 6 occurrences of GATTACCA, whereas we expect 1.53.
Is this level of over-representation significant or is it likely to result from chance?
Under the null hypothesis (would the sequence have been generated according to our background model), what would be the probability to observe at least 6 occurrences?
Binomial p-value
Probability distribution of k-mer occurrences in a sequence of length \(100,000\) according to a background model of identically and independently distributed nucleotides.
Left: probability mass function (PMF, density), i.e. the probability to observe exactly \(x\) occurrences. Arrow: observed occurrences.
Right panel: probability to observe at least X occurrences of the considered k-mer (note the logarithmic scale on Y). This is the P value of the occurrences.
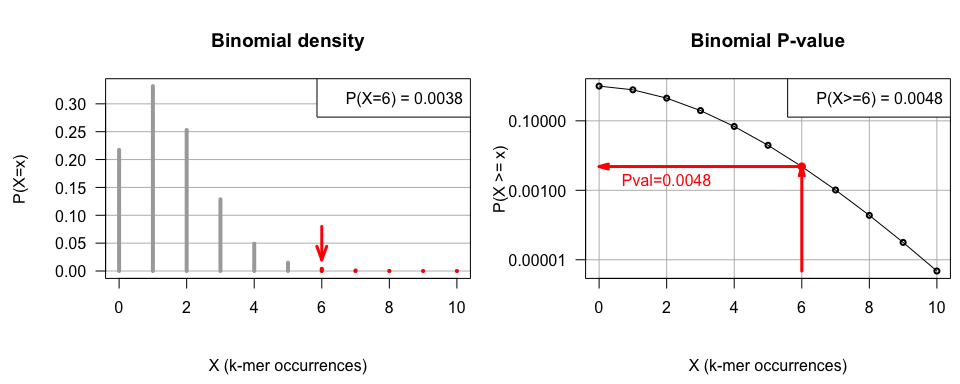
P value of k-mer over-representation
In our example, the P-value is the probability under the background model (equiprobable and independent nucleotides) that the occurrences of a k-mer (GATTACCA) would be equal to or higher than its observed value (\(x = 6\)).
We obtain the following result:
\[\begin{aligned}
P(X \ge x) &= \sum_{i=x}^{n}{C_n^i p^i (1-p)^{n-i}} \\
&= \sum_{i=6}^{100,000}{C_{100,000}^i 0.25^i (1-0.25)^{100,000-i}} \\
&= 0.00483
\end{aligned}\]
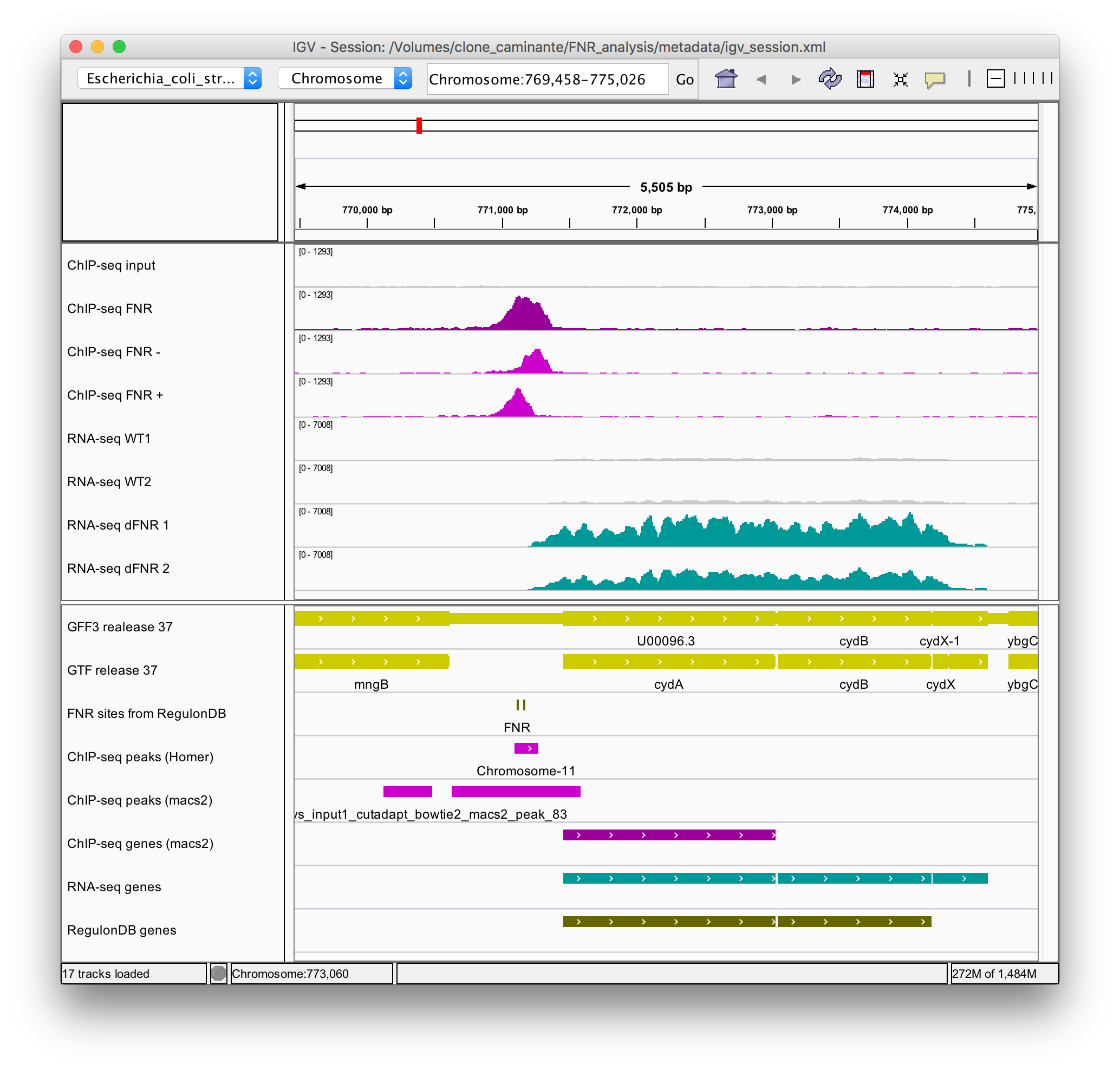
Problème : détection de pics ChIP-seq
Lors d’une expérience de ChIP-seq on a aligné \(N = 1.000.000\) lectures sur un génome de \(G = 4.000.000\) paires de bases. On découpe l’entièreté du génome en régions non-chevauchantes de \(w = 200\) pb et on compte le nombre de fragments de lecture par région. Sur une région donnée, on trouve \(x=70\) fragments de lecture. Peut-on considérer que cette région est significativement enrichie ?
- Quel est le nombre de régions génomiques considérées ?
- Quel est le nombre moyen de lectures par région de \(w = 200\) pb ?
- En supposant que les fragments de lecture snot répartis de façon aléatoire sur le génome, quelle serait la probabilité d’observer exactement 70 fragments de lecture sur une fenêtre donnée ?Choisissez une distribution pour modéliser ce problème en justifiant votre choix.
- Quelle est la P-valeur de cette observation ? Ecrivez la formule puis remplacez les symboles par les valeurs numériques (Le résultat du calcul sera fourni pendant le cours).
- Si l’on place un seuil \(\alpha = 0.05\) et qu’on analyse de la même façon toutes les régions non-chevauchantes de 200bp, combien de faux-positifs s’attend-on à trouver ?
Réponse
- Nombre de régions: \(T = G / w = 4.000.000 / 200 = 20.000\)
- Nombre moyen de lectures par région: \(\lambda = N / T = 1.000.000 / 20.000 = 50\)
- Probabilité d’occurrences: \(P(X = x) = \frac{\lambda^x}{x!}e^{-\lambda} = \frac{50^{70}}{70!}e^{-50} = 0.00136\)
- P-valeur:
\[\begin{aligned}
P(X \ge x) &= \sum_{i=x}^{\infty} \frac{\lambda^i}{i!}e^{-\lambda} = 1 - \sum_{i=0}^{x-1} \frac{\lambda^i}{i!}e^{-\lambda} \\
&= 1 - \sum_{i=0}^{69} \frac{50^i}{i!}e^{-50} = 0.00433
\end{aligned}\]
- E-valeur: \(E = P \cdot T = 0.00433 \cdot 20000 = 86.7\)
Tests multiples
Quelques exemples de tests multiples
| RNA-seq: détection de gènes différentiellement exprimés |
25.000 gènes |
| Détection de pics dans des données de ChIP-seq |
10.000.000 régions |
| Découverte de k-mères sur- ou sous-représentés dans les séquences régulatrices |
4096 6-mères, 16384 7-mères, 65536 8-mères |
| Etude d’association à échelle génomique |
1.000.000 SNPs |
| recherche de similarité de séquences avec BLAST |
1.000.000.000 |
Question: si on admet un seuil de \(5\%\) de faux-positifs sur chaque test, quel est le nombre de faux-positifs attendus ?
Nombre de faux-positifs attendus
La E-valeur (\(E\), E-value, expectation) est le nombre attendu de faux-positifs lorsqu’on effectue une série de tests avec un seuil donné sur la probabilité critique (\(P\)).
Elle est obtenue en multipliant la probabilité critique (\(P\)) par nombre de tests (\(T\)).
\[E = P \cdot T\]
Nombre de faux-positifs attendus : exemples
Nombre de faux-positif attendus pour \(\alpha = 0.05\).
| RNA-seq: détection de gènes différentiellement exprimés |
25.000 gènes |
1250 |
| Détection de pics dans des données de ChIP-seq |
10.000.000 régions |
500.000 |
| Découverte de k-mères sur- ou sous-représentés dans les séquences régulatrices |
4096 6-mères, 16384 7-mères, 65536 8-mères |
3276.8 |
| Etude d’association à échelle génomique |
1.000.000 SNPs |
50.000 |
| recherche de similarité de séquences avec BLAST |
1.000.000.000 |
50.000.000 |
Tableau de contingence
Dans un problème de prédiction ou de classification, on peut dresser un tableau de contingence indiquant la correspondance entre le statut réel de chaque test (sous hypothèse nulle \(H_0\) ou alternative \(H_1\)) et le résultat du test (positif ou négatif).
| Test |
+ |
\(FP\) |
\(TP\) |
|
- |
\(TN\) |
\(FN\) |
- \(FP\): False Positive
- \(TP\): True Positive
- \(TN\): True negative
- \(FN\): False Negative
Statistiques de contingence
False Positive Rate (FPR)
Le taux de faux positive (False Positive Rate , FPR) est la proportion de tests déclarés positifs parmi tous ceux menés sous hypothèse nulle.
\[FPR = \frac{FP}{H0} = \frac{FP}{FP+TP}\]
La P-valeur est une estimation du taux de faux-positifs attendu dans une batterie de tests.
|
|
H0
|
H1
|
|
Test positif
|
FP
|
TN
|
|
Test négatif
|
TP
|
FN
|
False Discovery Rate (FDR)
Le taux de fausse découverte (False Discovery Rate, FDR) est la proportion de faux-positifs parmi tous les tests déclarés positifs.
\[FDR = \frac{FP}{\text{Positiv}} = \frac{FP}{FP+TP}\]
On note par q-valeur l’estimation du taux de fausse découverte attendue à un niveau donné de p-valeur.
|
|
H0
|
H1
|
|
Test positif
|
FP
|
TN
|
|
Test négatif
|
TP
|
FN
|
Résumé des statistiques de contingence
| False Positive Rate |
FPR |
\(FPR = \frac{FP}{H0} = \frac{FP}{FP+TN}\) |
| False Discovery Rate |
FDR |
\(FDR = \frac{FP}{+} = \frac{FP}{FP+TP}\) |

Comment choisir un seuil pour la P-valeur ?